Easy-to-Hard Generalization: Scalable Alignment Beyond Human Supervision

Current AI alignment methodologies rely on human-provided demonstrations or judgments, and the learned capabilities of AI systems would be upper-bounded by human capabilities as a result. This raises a challenging research question: How can we keep improving the systems when their capabilities have surpassed the levels of humans? This paper answers this question in the context of tackling hard reasoning tasks (e.g., level 4-5 MATH problems) via learning from human annotations on easier tasks (e.g., level 1-3 MATH problems), which we term as \textiteasy-to-hard generalization. Our key insight is that an evaluator (reward model) trained on supervisions for easier tasks can be effectively used for scoring candidate solutions of harder tasks and hence facilitating easy-to-hard generalization over different levels of tasks. Based on this insight, we propose a novel approach to scalable alignment, which firstly trains the process-supervised reward models on easy problems (e.g., level 1-3), and then uses them to evaluate the performance of policy models on hard problems. We show that such \textiteasy-to-hard generalization from evaluators can enable \textiteasy-to-hard generalizations in generators either through re-ranking or reinforcement learning (RL). Notably, our process-supervised 7b RL model achieves an accuracy of 34.0% on MATH500, despite only using human supervision on easy problems. Our approach suggests a promising path toward AI systems that advance beyond the frontier of human supervision.

Three Important Things

1. Easy-to-Hard Generalization

How can we continue to supervise AI systems when they eventually attain superhuman-level status and we can no longer provide reliable labels?

This paper finds that reward models can be trained on easier tasks can be used to provide supervision signal for harder tasks.

Note that this differs from weak-to-strong generalization, where they found that strong learners trained on labels from weak teachers could achieve moderate performance gap recovered (PGR) in some settings like NLP tasks, but fails in others like reward modeling.

Their key insight that differs from weak-to-strong generalization is that evaluation is easier than generation.

2. How do generators generalize from easy to hard?

For their experiments, they use the MATH dataset, which has a difficulty of 1-5. They use 1-3 as the “easy” dataset, and 4-5 as “hard”.

They use the following setups for generators:

Full & Hard ICL: ICL using exemplars from either the entire MATH dataset, or just the hard ones
Easy-to-Hard ICL: ICL using exemplars from just easy problems, with the goal of evaluating if it can generalize to harder ones
Full SFT: SFT on tasks from all difficulty levels
Easy-to-Hard SFT: SFT on easy tasks only

And the results:

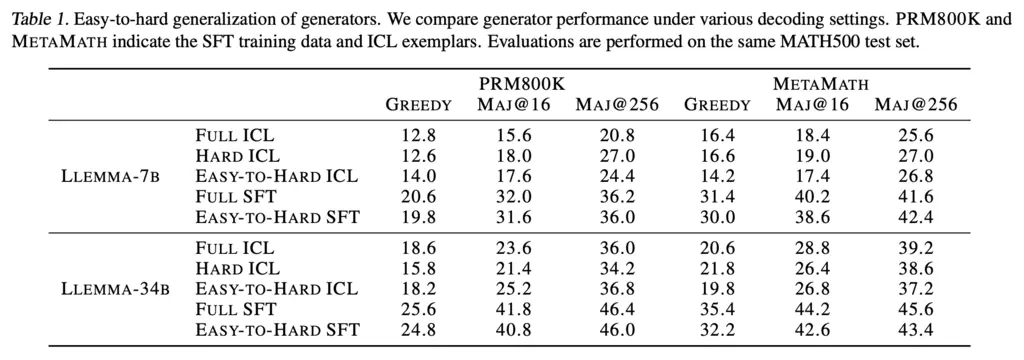
Unsurprisingly, SFT beats ICL.

They found that easy-to-hard gap also depends on the quality of SFT data used for training. In the lower-quality PRM800K, the difference between full SFT and easy-to-hard SFT was pretty small (~1%), but in the higher-quality MetaMath dataset, it went from 32.2 to 35.4 for Llemma-34B.

3. How do evaluators generalize from easy to hard?

On the other side, they consider the following setup for evaluators:

Final-Answer reward: gives binary reward based on accuracy of model’s answer
Outcome reward model (ORM): an outcome reward model is one that rewards models for the final answer. The reward model is trained to predict whether the solution is correct for every token (like a value model), and at inference time it is run on just the final token
Process reward model (PRM): this model predicts whether each CoT reasoning step (delimited by newlines) is correct
Outcome & process reward model (OPRM): best of both worlds - evaluates correctness of intermediate steps & also checking accuracy of final answer like ORM

To assess the performance of these techniques, they need a way to evaluate the evaluators. They do this by first sampling \(N\) solutions, and then using the evaluators to choose the best solution by the following methods: majority voting (only for final-answer model), and weighted voting and best-of-N using reward models.

The evaluator that can choose good solutions is deemed better.

Let’s first compare ORM/PRM/OPRM:

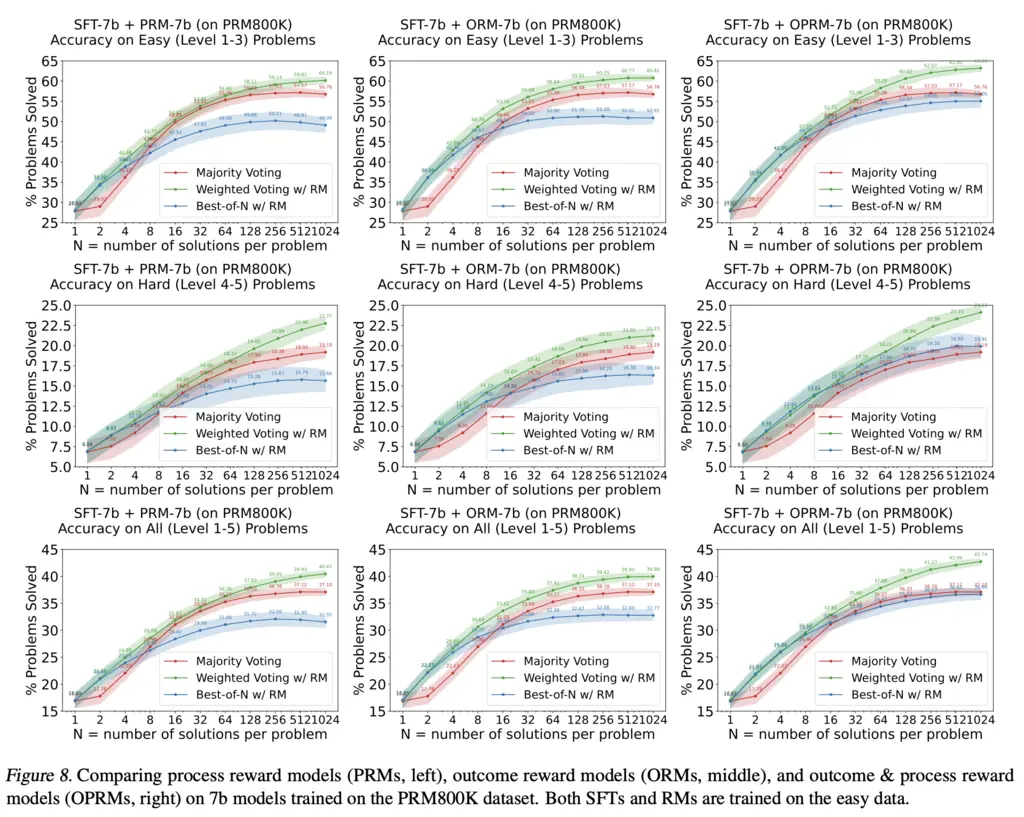
They found that ORM and PRM performs similarly, and OPRM outperforms the both of them.

Now comparing across difficulty of tasks:

They found that weighted voting outperforms best-of-N and majority voting. The former contradicts with previous work, which found minimal differences with RM best-of-N.

They also claimed that weighted voting resulted in better performance improvement gap for harder tasks, but this wasn’t really apparent to me visually as the gap seemed similar. They pointed to this as evidence that evaluators generalize better than generators.

4. Using Evaluators to Train Generators

If we accept that evaluators generalize better than generators, then we can use evaluators as reward models to train generators.

A surprising thing is that models trained with PRM rewards on just the easy tasks could actually outperform a model trained on all tasks, but without access to a PRM:

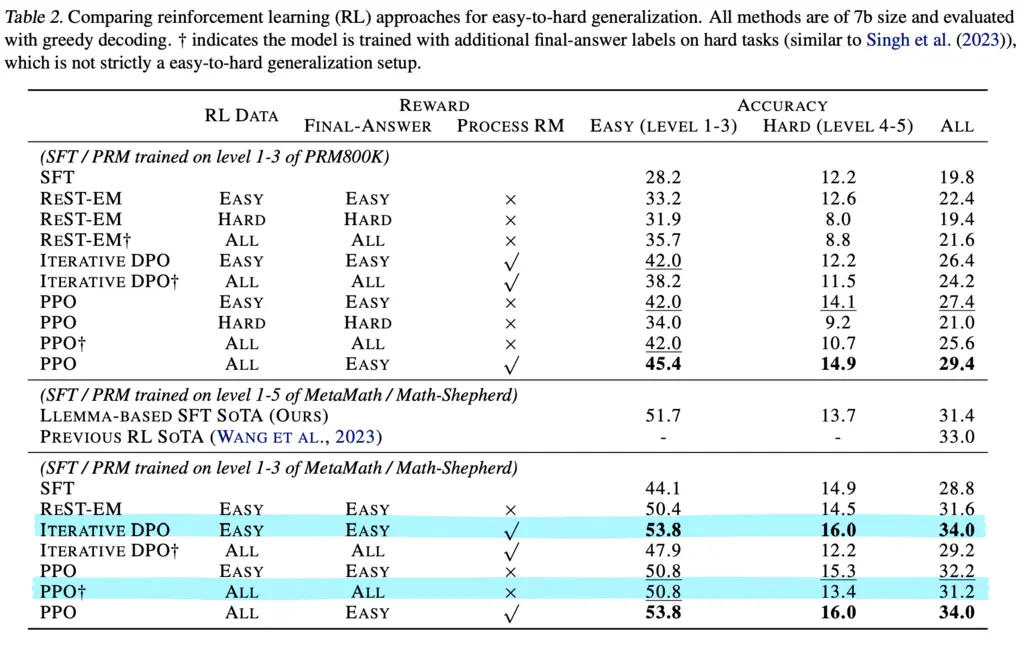
This includes the previous RL SOTA.

Most Glaring Deficiency

From an exposition standpoint, it was really hard to tell what the “big idea” of the paper was. It is dense and full of experiments, but sometimes it is hard to interpret the results and understand how it fits into their narrative.

This is kind of a minor point as it’s probably true by intuition, but I’m also not really convinced that their results demonstrates that evaluation is harder than generation. It seems hard to compare the two.

Conclusions for Future Work

A possible approach of training superhuman models is to use evaluators trained on easy data as a reward model to guide the generator that attempts hard problems. The problems of evaluating and generating are dual in some sense, but yet one is easier than the other, and we should exploit this fact.