Open-source Large Language Models are Strong Zero-shot Query Likelihood Models for Document Ranking

In the field of information retrieval, Query Likelihood Models (QLMs) rank documents based on the probability of generating the query given the content of a document. Recently, advanced large language models (LLMs) have emerged as effective QLMs, showcasing promising ranking capabilities. This paper focuses on investigating the genuine zero-shot ranking effectiveness of recent LLMs, which are solely pre-trained on unstructured text data without supervised instruction fine-tuning. Our findings reveal the robust zero-shot ranking ability of such LLMs, highlighting that additional instruction fine-tuning may hinder effectiveness unless a question generation task is present in the fine-tuning dataset. Furthermore, we introduce a novel state-of-the-art ranking system that integrates LLM-based QLMs with a hybrid zero-shot retriever, demonstrating exceptional effectiveness in both zero-shot and few-shot scenarios. We make our codebase publicly available at https://github.com/ielab/llm-qlm.

Three Important Things

1. Query Likelihood Models

Document ranking is usually performed by models fine-tuned on query-document datasets.

The paper proposes a new way of using LLMs to rank the relevance of documents for a supplied query. This is done by computing the probability of generating a query given a document, i.e its query likelihood:

\[S_{Q L M}(\boldsymbol{q}, d)=\frac{1}{|\boldsymbol{q}|} \sum_t \log \operatorname{LLM}\left(q_t \mid \boldsymbol{p}, d, \boldsymbol{q}_{<t}\right),\]

i.e the perplexity of the query given the document \(d\) and the model and prompt \(\boldsymbol{p}\).

The intuition is that the more relevant a query is to a document, the higher its query likelihood. They call this paradigm the query likelihood model (QLM).

2. Extending to Multi-shot Settings

The previous formulation is a zero-shot setting. To extend this to the multi-shot setting, they used the Guided by Bad Questions template (see InPars: Data Augmentation for Information Retrieval using Large Language Models).

In this template, 3 documents are provided, each accompanied by a bad and good question that pertains to it. This allows the model to learn what a good question should be.

3. Results

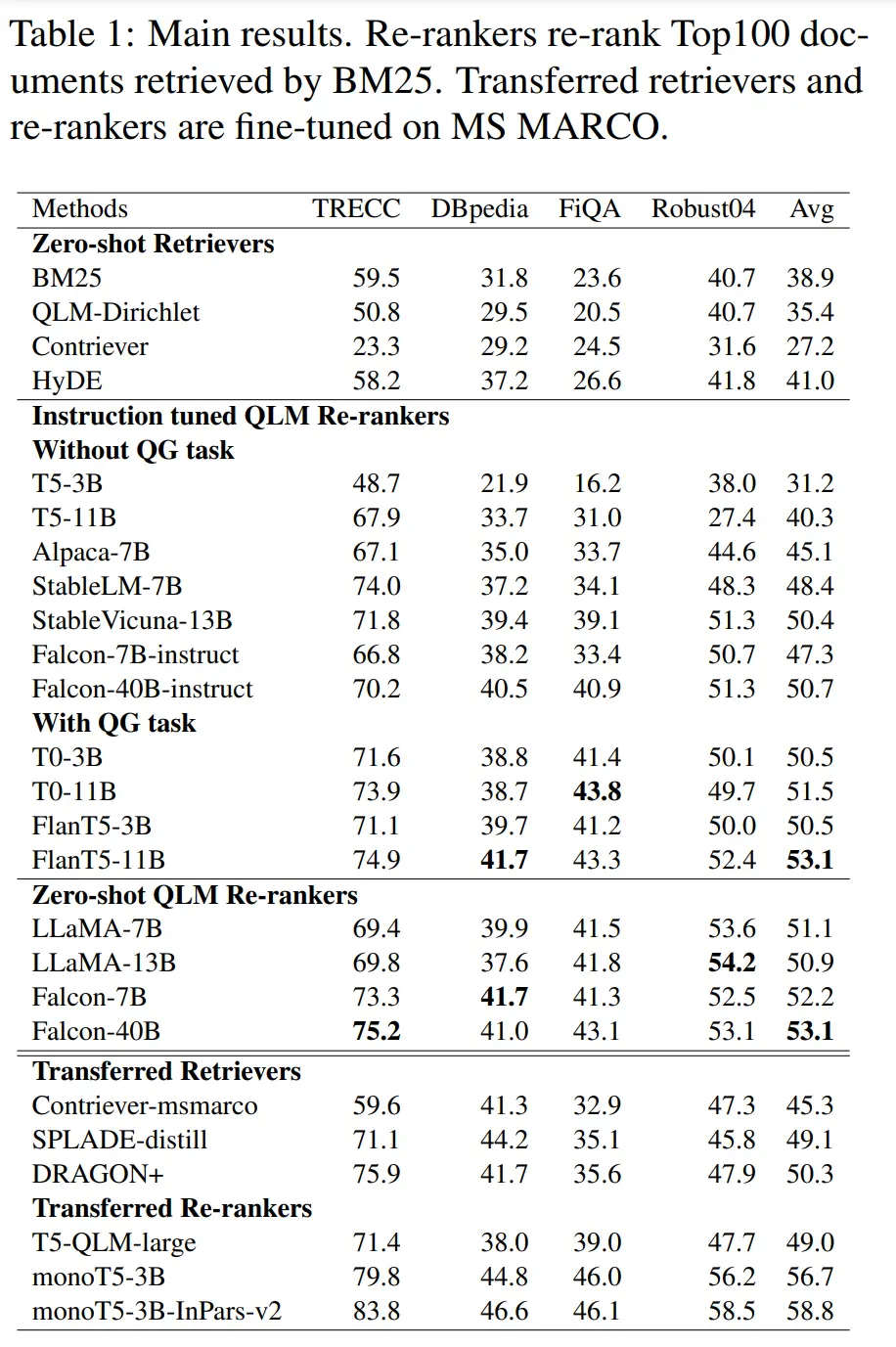
Zero-shot performance on pretrained-only models was surprisingly competitive. They also found that performance on instruction-tuned rerankers that did not contain question generation tasks were worse than zero-shot non-instruction tuned QLMs, indicating that instruction tuning could be harmful if the desired task was not reflected in its finetuning dataset.

Most Glaring Deficiency

Prompt format for the QLM was somewhat arbitrary. It’s also possible that the QLM may be sensitive to length, and there may be degenerate queries with low perplexity (i.e repeated phrases) but which are not actually relevant.

Conclusions for Future Work

Being able to compute a probability distribution allows you to sample from it. But sometimes, the values of the probability distribution itself could be useful!