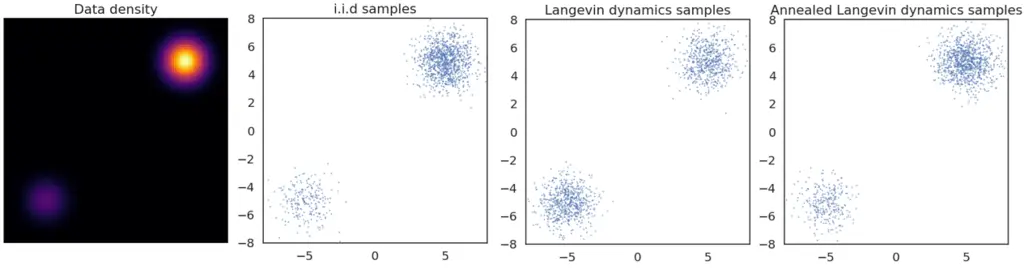
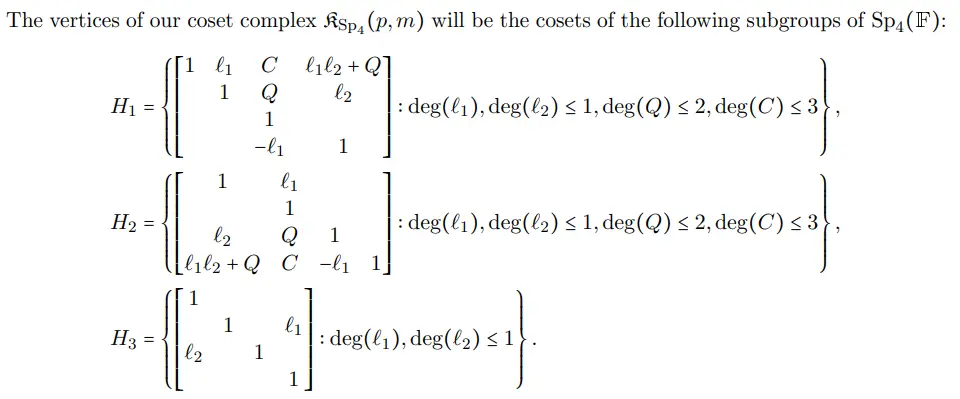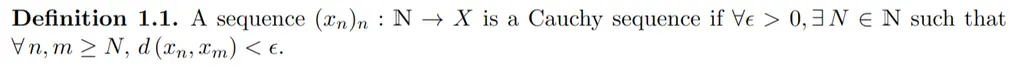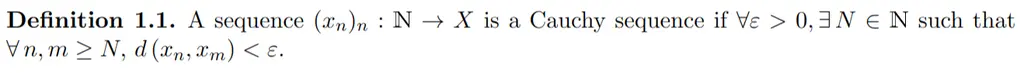This beginner’s guide will help to demystify the process of setting up Sound Voltex at home using a custom SDVX controller using Unnamed SDVX Clone.
My foray into rhythm games started way back with Love Live! School Idol Festival. While the game has sadly since shut down, other titles I’ve played include BanG Dream! and Project SEKAI.
When I visited Japan a few months ago in the summer, I discovered Sound Voltex, and instantly fell in love with its unique control system and beautiful flashy graphics:

In Japan, you pay 100 yen (~$0.68 USD) to play two to three songs. You get to play three songs if you don’t crash (i.e fail) any tracks, and two if you fail on either of the first two guaranteed plays.
Rhythm games in general are sadly not as mainstream outside of Japan. For instance, in Singapore I was only aware of a single arcade that had Sound Voltex cabs, even though arcades are quite popular in general. Similarly, in NYC, there’s only a single small arcade called Chinatown Fair that has Sound Voltex. So naturally I wanted to see if I could set it up at home to continue enjoying the game.
(Apparently, if you have a lot of disposable income and space in your living room, you can also just buy an entire previous-generation Sound Voltex cabinet for a few thousand dollars)
Why This Guide
I decided to write this guide since the setup process could seem somewhat daunting for people who are interested in rhythm games but are not developers. Hopefully now more people will also be able to play and enjoy this game.
The setup process is very straightforward on Windows, but has a few subtle points on macOS and Linux that I’ll point out.
Setup Specification
This guide will use the following setup:
- Game: unnamed-sdvx-clone, commonly abbreviated USC
- Controller: Yuancon SDVX controller.
While I performed the setup on macOS, the instructions are largely the same for Linux based systems as well. In fact, if you are already regardless of which controller or OS you use.
Installing Unnamed SDVX Clone
Windows
The setup process for Windows is very straightforward. You should just download the latest Windows build as linked on the Github page, and run usc-game.exe to start the game.
macOS
This is mostly just from the official instructions, but with implicit points made explicit:
- If you don’t have Homebrew on your machine yet, install it by following the instructions here. Homebrew is a package management software.
-
If you don’t have git yet, install it with Homebrew:
$ brew install gitGit is a version control system (normally used for code). In our case, we use it mainly to obtain the project dependencies.
-
Clone the
unnamed-sdvx-clonewithgit:$ git clone https://github.com/Drewol/unnamed-sdvx-cloneThis will result in the game being downloaded to a
unnamed-sdvx-clonefolder in your current working directory. -
Navigate into the new folder, and download the submodules of the project:
$ cd unnamed-sdvx-clone $ git submodule update --init --recursiveThis is necessary because the game has third-party dependencies, which are tracked as other Github repositories.
-
Install more dependencies required to build the project with Homebrew:
$ brew install cmake freetype libvorbis sdl2 libpng jpeg libarchive libiconvThese are all open source libraries required for the following reasons:
cmake: a popular build system used to compile the projectfreetype: for rendering fontslibvorbis: audio compressionsdl2: get access to hardware inputs like keyboard, mouse, controller, etclibpng: for using/manipulating PNG imagesjpeg: for using/manipulating JPEG imageslibarchive: compression librarylibiconv: convert between different character encodings (i.e ISO-8859-1 to UTF-8)
-
Configure the project using
cmake. In this case, the project author already kindly wrapped a script around this command, so we only have to run the script:$ ./mac-cmake.sh -
Compile and build the project:
$ makeThis step could take a while. If you want to speed it up, you can run it and specify the
-jargument parallelize the compilation based on the number of cores you have (use one less than your total number of cores):$ make -j 9 -
Run the game from the
binfolder:$ cd bin $ ./usc-gameIt is important to run it from the
./binfolder and not the root of the project directory, as some skins search for file dependencies in a relative manner and will hence not be able to find it.
Linux
Honestly if you’re on Linux, you should be able to figure it out by yourself 😊
First Startup
On first startup, you should see this:
For now, you can just use your mouse to interact with the game menu.
Configuring The Controller
Let’s now setup our Yuancon controller!
-
Quit the game, and unplug your SDVX controller if it is plugged in
-
Hold the
STARTandBT-Cbutton simultaneously. TheSTARTbutton is the diamond-shaped button at the top, while the BT-C is the third white button from the left (it should also be labelled on the controller board).Then while still holding down both buttons, connect it to your computer. This will put it in Controller HID Mode, where the controller inputs as a gamepad.
-
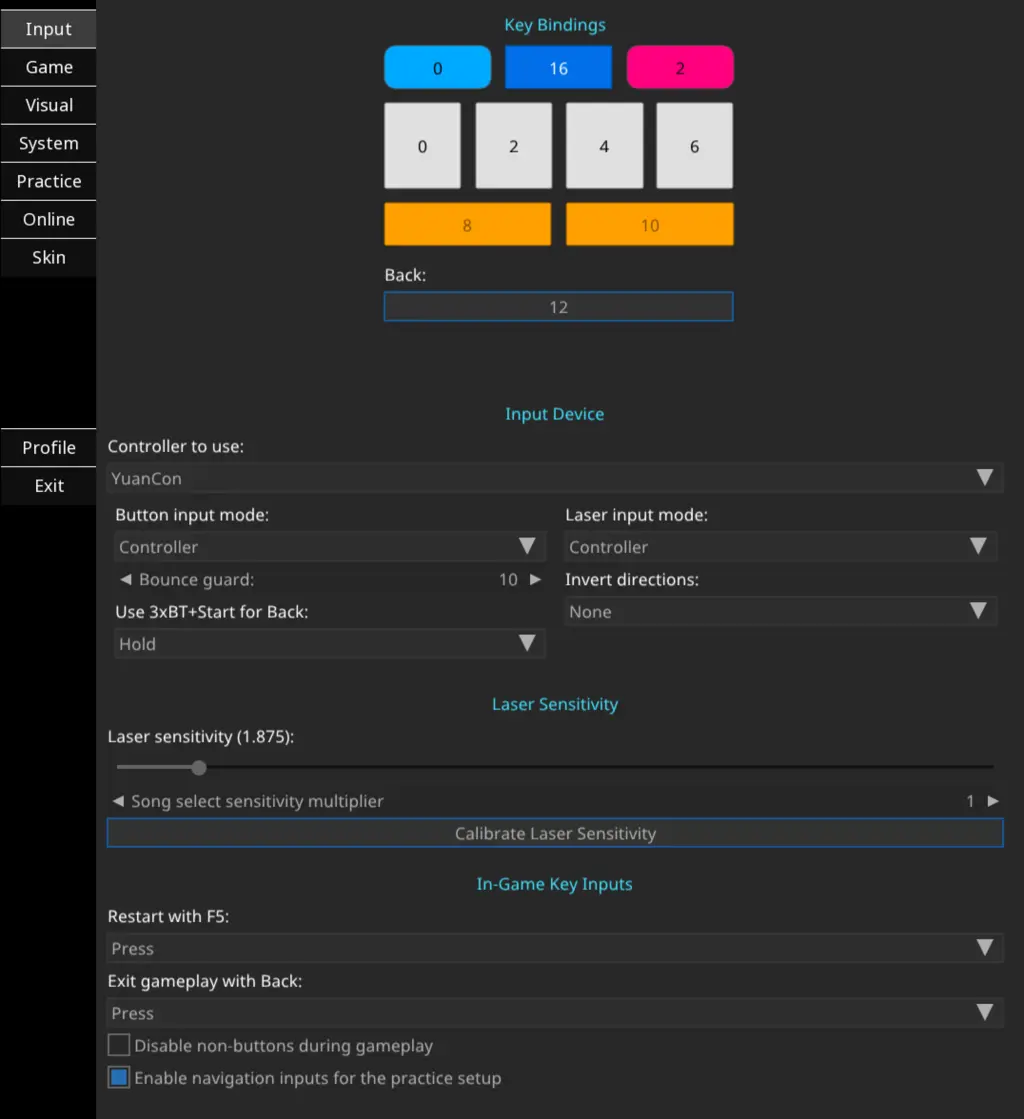
Start up the game again, and navigate to the
Settingspage. Here, you want to do the following:- Set
Button input modetoController - Set
Laser input modetoController - Adjust laser sensitivity accordingly (I like
1.875) - Click on each of the key bindings, and hit the corresponding keys on your controller. I used the button on the right side of the controller panel as my back button.
You should have something that looks similar to this:
- Set
-
Restart the game. You should now be able to use the knobs to cycle through the menus, and the buttons to activate them!
Getting Songs
Right after setup, there are no songs to play yet. USC uses the same chart format as K-Shoot MANIA (KSM)
There are a few places you can get songs:
- Nautica hosts community-created KSM charts. There is also a menu option to download these directly from within USC.
- Converted SDVX Charts: probably somewhat questionable legally because of copyright and whatnot but a lot of people recommend and use it
- This KSM FAQ page on Reddit provides many useful links for downloading new songs
Once you have downloaded the songs, unzip and extract them if necessary, and copy them into ./bin/songs.
Skinning The Game
The default skin works, but it is not very impressive:
Let’s try to re-create the original SDVX arcade experience with skins. You can get skins for the game here. These are really high-effort and well-made, and huge thanks to the developers and artists for making them.
Once you have downloaded the skin, extract and move them to ./bin/skins. You should then be able to select the skin under the Skins tab of the game settings.
The UI of the skin for the game may change depending on whether your monitor is in portrait or landscape mode. Orienting it vertically is recommended for the best SDVX-like experience - the spaceship(?) at the bottom only shows up when it’s vertical.
Some examples of the different skins are shown below. I know, they’re pretty!
(Why are the previews so low-res? Bandwidth costs add up!)
LiqidWave
If you run into errors about shaders when trying to play a song, see the Common Errors section below.
ExperimentalGear
As a side note, if you find the default menu text for this skin too casual/unprofessional, you can change it in ./bin/skins/ExperimentalGear/scripts/language/EN.lua.
Heavenly Express
Crew
Not all skins come with a cast of crews, like the ExperimentalGear skin which only comes with a boring empty nothing skin in ./bin/skins/ExperimentalGear/textures/crew/anim.
As crews are very important for our psychological safety and well-being, fortunately we can just copy over the animations from other skins. In HeavenlyExpress, you can find it in ./bin/skins/HeavenlyExpress-1.3.0/textures/_shared/crew. Similarly, in LiqidWave they are stored in ./bin/skins/LiqidWave-1.5.0/textures/_shared/crew.
Conclusion
If you’ve made it this far, congrats and thanks for reading! I hope you’ll enjoy the game as much as I do. If you have any questions or run into problems, feel free to ask in the comments section below.
Extras
Aside: KSM Chart Formats
KSM charts have a .ksh extensions. This can be a useful check to ensure that any charts that you download are actually for this game.
The following is a snippet of the ADV.ksh (i.e advanced beatmap) file for YOASOBI’s Idol (アイドル):
title=アイドル
artist=YOASOBI /「推しの子」より
effect=AS
jacket=jk.jpg
illustrator=-
difficulty=challenge
level=10
t=166
m=music.ogg
o=0
bg=desert
layer=smoke
po=56024
plength=15000
pfiltergain=50
filtertype=peak
chokkakuautovol=0
chokkakuvol=50
ver=171
--
beat=4/4
0000|00|--
--
0000|00|0-
0000|00|:-
0000|00|o-
0000|00|:-
0000|00|:-
0000|00|:-
0000|00|:-
0000|00|:-
0000|00|:-
0000|00|:-
0000|00|:-
0000|00|:-
0000|00|:-
0000|00|:-
0000|00|:-
0000|00|:-
0000|00|o-
0000|00|:-
0000|00|:-
0000|00|:-
0000|00|:-
0000|00|:-
0000|00|:-
0000|00|:-
0000|00|:-
0000|00|:-
0000|00|:-
0000|00|:-
0000|00|:-
0000|00|:-
0000|00|:-
0000|00|:-
0000|00|P-
0000|00|:-
0000|00|:-
0000|00|:-
0000|00|:-
0000|00|:-
0000|00|:-
0000|00|:-
0000|00|:-
0000|00|:-
0000|00|:-
0000|00|:-
0000|00|:-
0000|00|:-
0000|00|:-
0000|00|:-
0000|00|P-
0000|00|:-
0000|00|:-
0000|00|:-
0000|00|:-
0000|00|:-
0000|00|:-
0000|00|:-
0000|00|:-
0000|00|:-
0000|00|:-
0000|00|:-
0000|00|:-
0000|00|:-
0000|00|:-
0000|00|:-
--
0000|00|0-
0000|00|:-
filtertype=lpf1
0000|00|0o
0000|00|::
0000|00|o0
0000|00|::
Possible Errors And How To Resolve
Some errors I faced when trying to setup and configure the game.
module commonShared not found
If you get a Lua error about not being able to load a commonShared package, such as when using a custom skin:
[14:45:10][Error] Lua error: ...clone/bin/skins/HeavenlyExpress-1.3.0/scripts/common.lua:2: module 'commonShared' not found:
no field package.preload['commonShared']
no file '/usr/local/share/lua/5.3/commonShared.lua'
no file '/usr/local/share/lua/5.3/commonShared/init.lua'
no file '/usr/local/lib/lua/5.3/commonShared.lua'
no file '/usr/local/lib/lua/5.3/commonShared/init.lua'
no file './commonShared.lua'
no file './commonShared/init.lua'
no file '/Users/fanpu/unnamed-sdvx-clone/bin/skins/HeavenlyExpress-1.3.0/scripts/commonShared.lua'
no file 'skins/HeavenlyExpress-1.3.0/textures/_shared/scripts/commonShared.lua'
no file '/usr/local/lib/lua/5.3/commonShared.so'
no file '/usr/local/lib/lua/5.3/loadall.so'
no file './commonShared.so'
You are likely running the game from the root of the project directory (i.e ./bin/usc-game), instead of from within the ./bin directory itself.
HeavenlyExpress Skin: Could not load shaders
If you are using the HeavenlyExpress skin, you may run into the following error after selecting a track to play:
Shader Error:
Could not load shaders skins/HeavenlyExpress-1.3.0/shaders/holdbutton.vs
and skins/HeavenlyExpress-1.3.0/shaders/holdbutton.fs
You may also get logs like this:
[14:58:37][Error] Shader program compile log for /Users/fanpu/unnamed-sdvx-clone/bin/skins/HeavenlyExpress-1.3.0/shaders/holdbutton.vs: ERROR: 0:6: 'varying' : syntax error: syntax error
[14:58:37][Error] Shader program compile log for /Users/fanpu/unnamed-sdvx-clone/bin/skins/HeavenlyExpress-1.3.0/shaders/holdbutton.fs: ERROR: 0:10: 'varying' : syntax error: syntax error
[14:58:37][Error] Failed to load vertex shader for material from /Users/fanpu/unnamed-sdvx-clone/bin/skins/HeavenlyExpress-1.3.0/shaders/holdbutton.vs
The shaders were probably written a long time ago, since the varying keyword has been deprecated since OpenGL 3.3. It was previously used as a qualifier for variables that communicate between the vertex shader and the fragment shader, that is now replaced by the in and out qualifiers to provide a more clear distinction of data flow between shaders.
To fix this, modify the two files and change the varying keyword to out in both files:
In file bin/skins/HeavenlyExpress-1.3.0/shaders/holdbutton.vs:
#version 330
#extension GL_ARB_separate_shader_objects : enable
layout(location=0) in vec2 inPos;
layout(location=1) in vec2 inTex;
out vec4 position; // update here
out gl_PerVertex
{
vec4 gl_Position;
};
...rest of file omitted...
In file bin/skins/HeavenlyExpress-1.3.0/shaders/holdbutton.fs:
#version 330
#extension GL_ARB_separate_shader_objects : enable
layout(location=1) in vec2 fsTex;
layout(location=0) out vec4 target;
uniform sampler2D mainTex;
uniform float objectGlow;
out vec4 position; // update here
...rest of file omitted...
Restart the game and you should be good now.
ExperimentalGear Custom Skin Does Not Change
I faced issues where it appeared that the value that I set in the settings page for the skin to use was not being saved. I resolved this by manually editing the config file in ./bin/skins/ExperimentalGear/skin.cfg.